注意：此页面搜索的是所有试题
佳木斯大学语言治疗学
目标管理是谁首先提出来的（ ）
·彼得·德鲁克
·法约尔
·马斯洛
·孔茨
设A是B的真子集,则( )
·
·
·
·
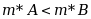
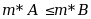
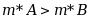
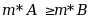
函数列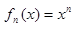
在[0，1]上（ ）于0.
·几乎处处一致收敛
·收敛
·一致收敛
·基本一致收敛
·
·
·
·
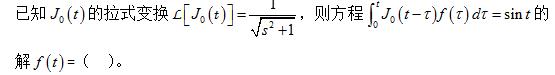
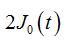
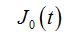
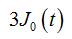
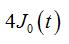
设E是Rn中的可测集，f(x)为E上的可测函数，若
，则（ ）
·在E上，f(z)不一定恒为零
·在E上，f(z)≥0
·在E上,f(z)=0
·在E上,f(z)≠0
设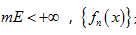
是E上几乎处处有限的可测函数列，f(x)是E上几乎处处有限的可测函数，则
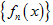几乎处处收敛于f(x)是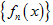依测度收敛于f(x)的（ ）
·必要条件
·充分条件
·充分必要条件
·无关条件
关于连续函数与可测函数，下列论述中正确的是（ ）
·它们是同一概念
·<em>a</em>, <em>e</em>有限的可测函数是连续函数
·<em>a</em>, <em>e</em>有限的可测函数是基本上连续的函数
·<em>a</em>, <em>e</em>有限的可测函数是<em>a</em>, <em>e</em>连续的函数
·
·
·
·
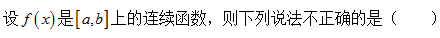
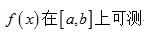
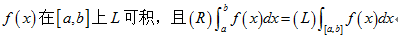
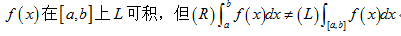
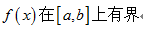
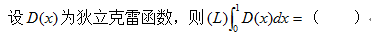
·0
·1
·1/2
·不存在
设E是闭区间[0,1]中的无理点集，则（ ）
·mE=1
·mE=0
·E是不可测集
·E是闭集
若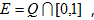
则mE=（）
·0
·1
·2
·3
设<em>E</em>是[0，1]中的不可测集，
则下列函数在[0，1]上可测的是（）.
·<em>f</em>(<em>x</em>)
·<em>f +</em>(<em>x</em>)
·|<em> f</em>(<em>x</em>)|
·<em>f</em> -(<em>x</em>)
关于依测度收敛,下列说法中不正确的是
·依测度收敛不一定一致收敛
·依测度收敛不一定收敛
·若{fn(x)}在E上a.e.收敛于a.e.有限的可测函数f (x), 则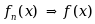
·若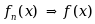,则存在子列
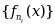a. e.收敛于f (x).
设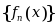
是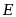
上一列非负可测函数,则
·
·
·
·
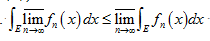
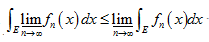
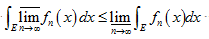
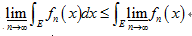
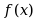在可测集
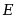上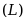
可积的必要条件是,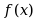为____.( )
·连续函数
·几乎处处连续函数
·单调函数
·几乎处处有限的可测函数
·彼得·德鲁克
·法约尔
·马斯洛
·孔茨
设A是B的真子集,则( )
·
·
·
·
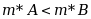
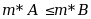
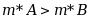
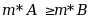
函数列
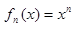在[0，1]上（ ）于0.·几乎处处一致收敛
·收敛
·一致收敛
·基本一致收敛
·
·
·
·
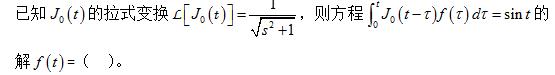
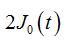
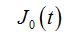
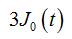
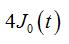
设E是Rn中的可测集，f(x)为E上的可测函数，若
，则（ ）·在E上，f(z)不一定恒为零
·在E上，f(z)≥0
·在E上,f(z)=0
·在E上,f(z)≠0
设
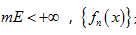是E上几乎处处有限的可测函数列，f(x)是E上几乎处处有限的可测函数，则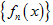几乎处处收敛于f(x)是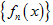依测度收敛于f(x)的（ ）·必要条件
·充分条件
·充分必要条件
·无关条件
关于连续函数与可测函数，下列论述中正确的是（ ）
·它们是同一概念
·<em>a</em>, <em>e</em>有限的可测函数是连续函数
·<em>a</em>, <em>e</em>有限的可测函数是基本上连续的函数
·<em>a</em>, <em>e</em>有限的可测函数是<em>a</em>, <em>e</em>连续的函数
·
·
·
·
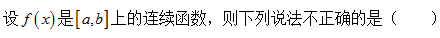
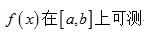
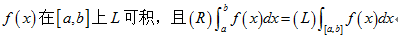
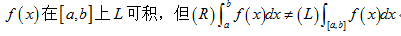
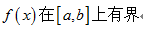
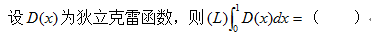
·0
·1
·1/2
·不存在
设E是闭区间[0,1]中的无理点集，则（ ）
·mE=1
·mE=0
·E是不可测集
·E是闭集
若
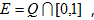则mE=（）·0
·1
·2
·3
设<em>E</em>是[0，1]中的不可测集，
则下列函数在[0，1]上可测的是（）.·<em>f</em>(<em>x</em>)
·<em>f +</em>(<em>x</em>)
·|<em> f</em>(<em>x</em>)|
·<em>f</em> -(<em>x</em>)
关于依测度收敛,下列说法中不正确的是
·依测度收敛不一定一致收敛
·依测度收敛不一定收敛
·若{fn(x)}在E上a.e.收敛于a.e.有限的可测函数f (x), 则
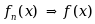
·若
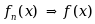,则存在子列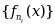a. e.收敛于f (x).设
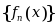是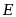上一列非负可测函数,则 ·
·
·
·
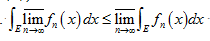
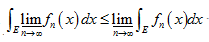
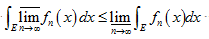
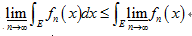
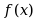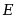在可测集上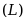可积的必要条件是,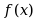为____.( )·连续函数
·几乎处处连续函数
·单调函数
·几乎处处有限的可测函数