注意:此页面搜索的是所有试题
石家庄铁道大学线性代数
以下运算规律,表述不正确的是( )( 2.000分)
A、 A+B=B+A
B、 (A+B)+C=A+(B+C)
C、 A+0=A,A+(-A)=0
D、 A-B=A+B
下列说法不正确的是( )( 2.000分)
A、 向量组线性相关→任一个向量可由其余向量线性表示
B、 向量组线性无关→任何一个向量都不能由其余向量线性表示
C、 若B可以由A线性表示且r < s,则B线性相关
D、 若A 、B可以互相线性表示且A 、B 都线性无关,则r = s
设A是m×n矩阵,Ax=0是非齐次方程组Ax=b对应的齐次方程组.下列结论正确的是 .( 2.000分)
A、 若Ax=0仅有零解,则Ax=b有唯一解
B、 若Ax=0有非零解,则Ax=b有无穷多解
C、 若Ax=b有无穷多解,则Ax=0仅有零解
D、 若Ax=b有无穷多解,则Ax=0有非零解
已知方程组当a=,该方程组有非零解

A、 a=2,b=1
B、 a=-2,b=0
C、 a=1,b=0
D、 a=2,b=-1
已知方程组,下列不属于该方程组的解的是
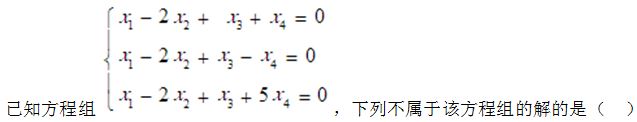
已知矩阵A=,则矩阵A经过对角化后,得到的对角矩阵是
已知向量组α1=(a,2,1),α2=(2,a,0),α3=(1,-1,1),当a=( )时,向量组α1,α2,α3,线性相关。( 2.000分)
A、 a=3或a=2
B、 a=3或a=-2
C、 a=2或a=5
D、 a=-3或a=-2
向量组a1=的线性相关性为
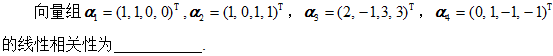
A、 线性相关
B、 线性无关
C、 不能判定
D、 与向量的维数有关
已知矩阵A=则其逆矩阵是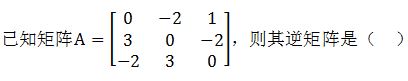
行列式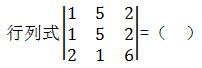
A、 30
B、 -30
C、 1
D、 0
经过运算5A-2B,得到一个新的矩阵,则该新矩阵第三行第二列的元素是( )( 2.000分)
A、 5
B、 -5
C、 3
D、 -7
若A为3阶方阵,且λ=0为其一特征值,则A的秩
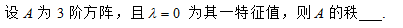
A、 0
B、 1
C、 2
D、 都可能
已知齐次线性方程组,若该方程组有非零解,则
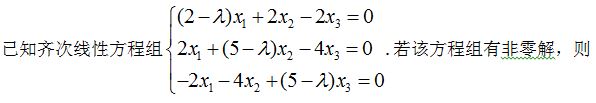
λ=( )( 2.000分)
A、 2或8
B、 3或10
C、 1或9
D、 1或10
利用逆矩阵求解方程组,则其解为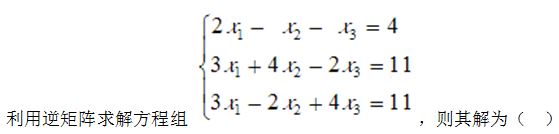
A、 .x1=3,x2=1,x3=1
B、 x1=3,x2=2,x3=1
C、 x1=1,x2=1,x3=1
D、 x1=3,x2=1,x3=2
已知矩阵A=,则矩阵A经过对角化后,得到的对角矩阵是
A、 A+B=B+A
B、 (A+B)+C=A+(B+C)
C、 A+0=A,A+(-A)=0
D、 A-B=A+B
下列说法不正确的是( )( 2.000分)
A、 向量组线性相关→任一个向量可由其余向量线性表示
B、 向量组线性无关→任何一个向量都不能由其余向量线性表示
C、 若B可以由A线性表示且r < s,则B线性相关
D、 若A 、B可以互相线性表示且A 、B 都线性无关,则r = s
设A是m×n矩阵,Ax=0是非齐次方程组Ax=b对应的齐次方程组.下列结论正确的是 .( 2.000分)
A、 若Ax=0仅有零解,则Ax=b有唯一解
B、 若Ax=0有非零解,则Ax=b有无穷多解
C、 若Ax=b有无穷多解,则Ax=0仅有零解
D、 若Ax=b有无穷多解,则Ax=0有非零解
已知方程组当a=,该方程组有非零解
A、 a=2,b=1
B、 a=-2,b=0
C、 a=1,b=0
D、 a=2,b=-1
已知方程组,下列不属于该方程组的解的是
已知矩阵A=,则矩阵A经过对角化后,得到的对角矩阵是
已知向量组α1=(a,2,1),α2=(2,a,0),α3=(1,-1,1),当a=( )时,向量组α1,α2,α3,线性相关。( 2.000分)
A、 a=3或a=2
B、 a=3或a=-2
C、 a=2或a=5
D、 a=-3或a=-2
向量组a1=的线性相关性为
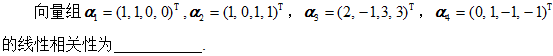
A、 线性相关
B、 线性无关
C、 不能判定
D、 与向量的维数有关
已知矩阵A=则其逆矩阵是
行列式
A、 30
B、 -30
C、 1
D、 0
经过运算5A-2B,得到一个新的矩阵,则该新矩阵第三行第二列的元素是( )( 2.000分)
A、 5
B、 -5
C、 3
D、 -7
若A为3阶方阵,且λ=0为其一特征值,则A的秩
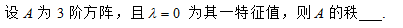
A、 0
B、 1
C、 2
D、 都可能
已知齐次线性方程组,若该方程组有非零解,则
λ=( )( 2.000分)
A、 2或8
B、 3或10
C、 1或9
D、 1或10
利用逆矩阵求解方程组,则其解为
A、 .x1=3,x2=1,x3=1
B、 x1=3,x2=2,x3=1
C、 x1=1,x2=1,x3=1
D、 x1=3,x2=1,x3=2
已知矩阵A=,则矩阵A经过对角化后,得到的对角矩阵是